Deep-Model Reference Adaptive Control
Abstract:
We present a new neuroadaptive architecture: Deep Neural Network-based Model Reference Adaptive Control (DMRAC). Our architecture utilizes the power of deep neural network representations for modeling significant nonlinearities while marrying it with the boundedness guarantees that characterize MRAC based controllers. We demonstrate that DMRAC can subsume previously studied learning-based MRAC methods, such as concurrent learning and GP-MRAC. This makes DMRAC a highly powerful architecture for high-performance control of nonlinear systems with long-term learning properties.
please refer to post Model Reference Adaptive Control for basics of MRAC
Introduction
One significant design choice in MRAC architecture is the selection of feature vector for unstructured uncertainty case. In Model Reference Adaptive Control article, we showed empirically that the choice of the feature vector in the adaptive element directly affected the system capability to approximate the uncertainties. Using system state \(x(t)\) as features resulted in a very poor estimate of uncertainty, and reference tracking, whereas RBF feature need operating domain knowledge for hyperparameter tuning.
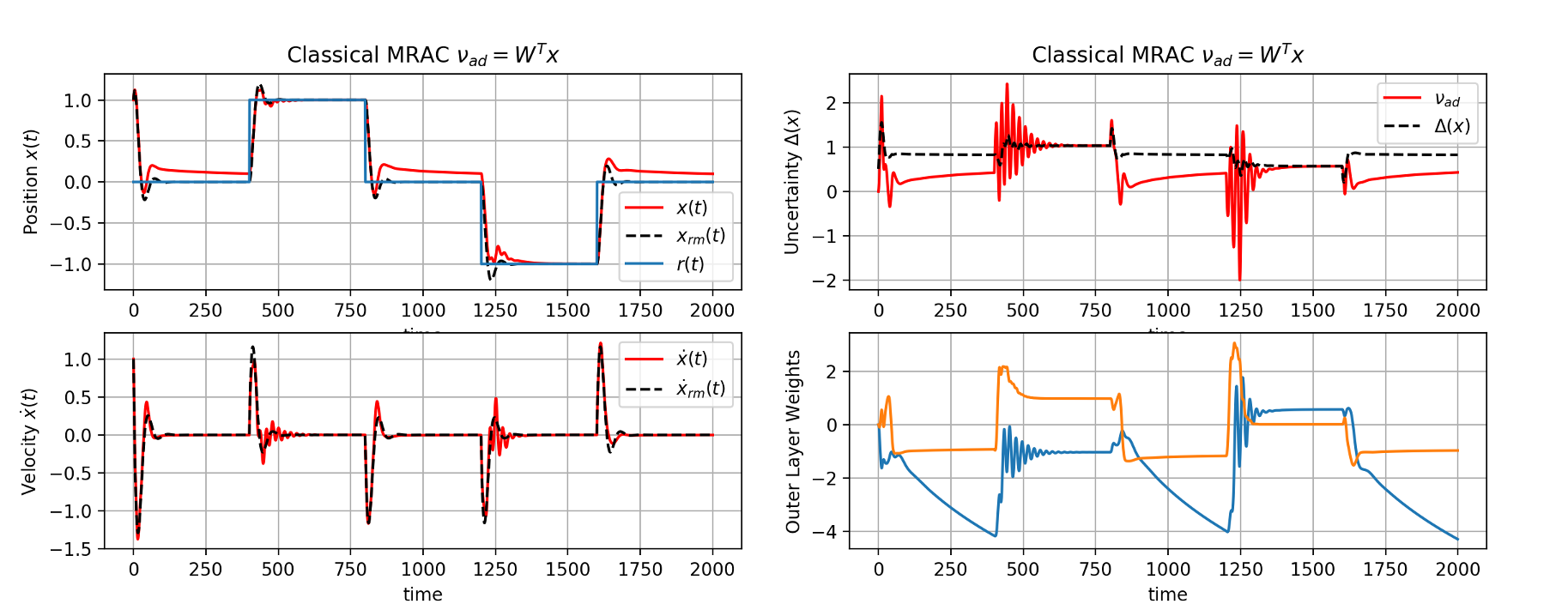
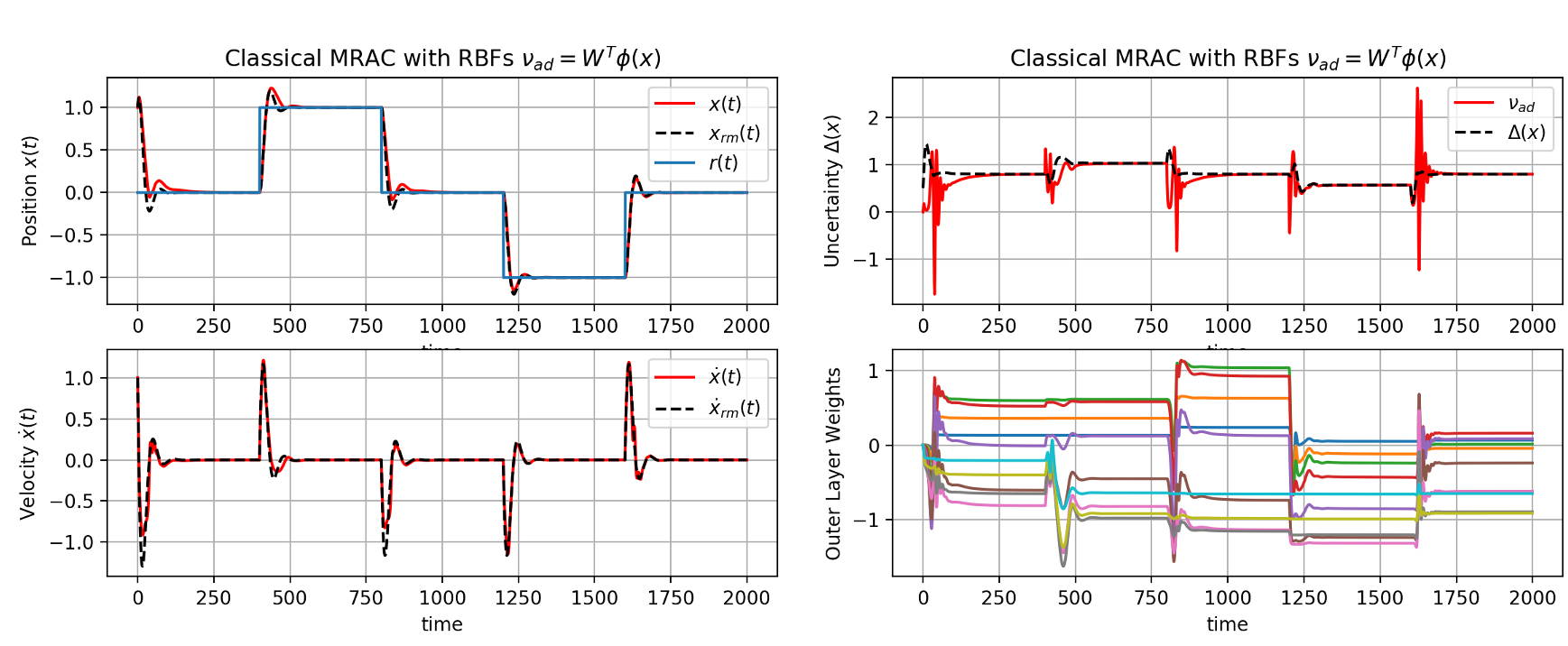
To alleviate this issue, Chowdhary et al. presented a Gaussian Process Model Reference Adaptive Controller. Gaussian Process (GP)-MRAC utilizes a GP as a model of uncertainty. A GP is a Bayesian nonparametric adaptive element that can adapt both its weights and the structure of the model in response to the data. GP-MRAC has strong long-term learning properties as well as high control performance (Refer Gaussian Process Model Reference Adaptive Controller with Generative Network).
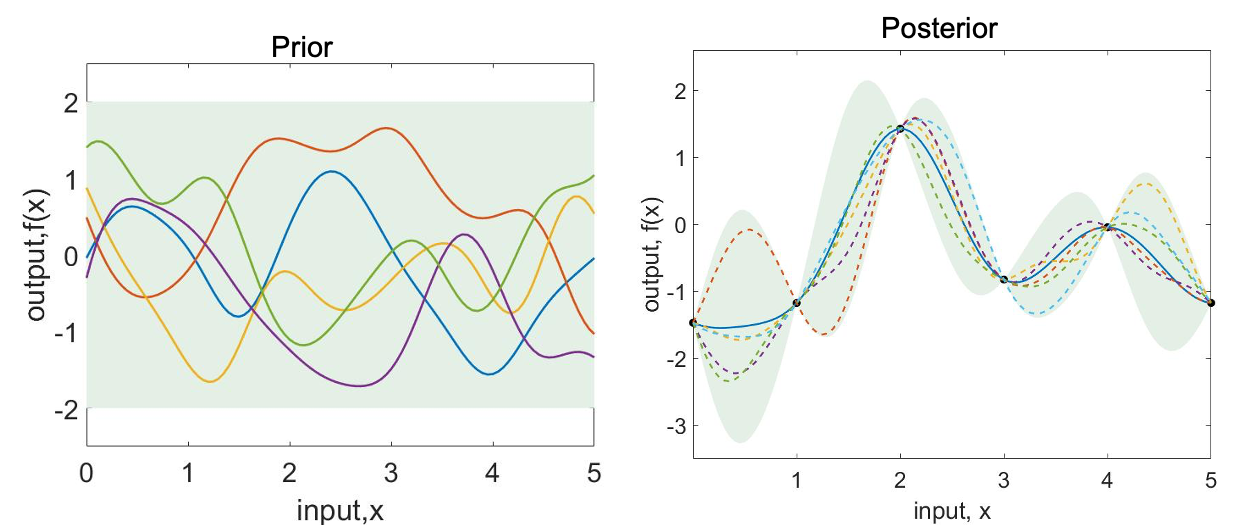
However, GPs can be viewed as “shallow” machine learning models, and do not utilize the power of learning complex features through compositions as deep networks do. Hence, one wonders whether the power of deep learning could lead to even more powerful learning-based MRAC architectures than those utilizing GPs.
Deep Neural Networks (DNN) have lately shown tremendous empirical performance in many applications, including fields such as computer vision, speech recognition, translation, natural language processing, Robotics, Autonomous driving, and many more. Unlike their counterparts, such as Gaussian Radial Basis Function networks, deep networks learn features by learning the weights of nonlinear compositions of weighted features arranged in a directed acyclic graph. It is now pretty clear that deep neural networks are outshining heuristic-based regression and classification algorithms as well as RBFNs, GPs, Single Hidden layer-NNs, and other classical machine learning techniques. However, their utility in the context of control, and especially safety-critical control, which requires stability guarantees, has been an open question.
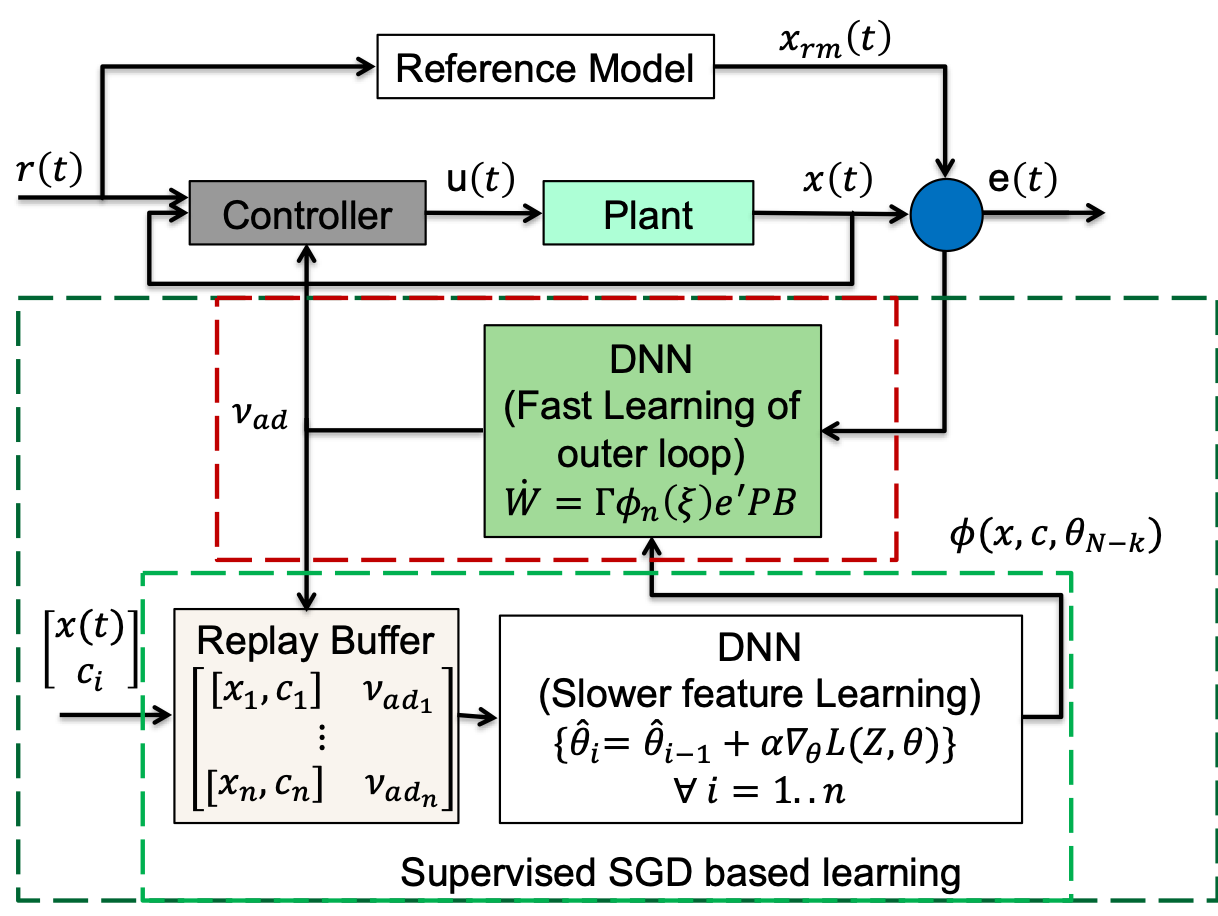
This article presents a control architecture and flight test results of Deep Neural Network MRAC (DMRAC). However, for the details of DMRAC controller, the algorithm for the online update of the weights of the DNN by utilizing a dual time-scale adaptation scheme, stability guarantees and Uniform Ultimate Boundedness (UUB) of the entire DMRAC controller refer to our paper Deep Model Reference Adaptive Control
DMRAC controller aims to enforce the unknown nonlinear dynamic system to track a designed reference model given as
\[\begin{align*} \dot{x}(t) &= f(x)+Bu(t) \\ \dot{x}_{rm}(t) &= A_{rm}x_{rm}(t)+B_{rm}r(t) \end{align*}\]Where \(x(t) \in \mathcal{D}_x \in \mathbb{R}^n\), \(u(t) \in \mathbb{R}^m\) and \(f: \mathbb{R}^n \rightarrow \mathbb{R}^n\) is Lipschitz.
The control is designed to be of the form \(u(t) = -kx(t)+k_gr(t)-\nu_{ad}\), Where \(k, k_g\) are designed to satisfy the following matching condition \(A_{rm} = A-Bk, B_{rm}=Bk_g\)
DMRAC model uncertaintaties as deep neural network,
\[\begin{align*} \nu_{ad}(x) = W^T\phi_n(\theta_{n-1},\phi_{n-1}(\theta_{n-2},\phi_{n-2}(...)))) \end{align*}\]We separate the network weights as outer layer weights \(W\) and inner-layer weights \(\theta_n\). The inner layer weights are updated using stochastic gradient descent over replay buffer collected over previous data.
\begin{equation} L(\boldsymbol{Z, \theta}) = \frac{1}{M}\sum_i^M \ell(\boldsymbol{Z_i, \theta}) \label{empirical_loss} \end{equation}
\begin{equation} \boldsymbol{\theta}_{k+1} = \label{SGD2} \end{equation} Where \(L(\boldsymbol{Z, \theta})\) empirical estimate of \(\ell_2\) cost function over data.
The outer layer weights of DMRAC are updated using MRAC rule.
\[\begin{align*} \dot{W} = -\Gamma\phi_n(x)e(t)^TPB \end{align*}\]The total controller flow diagram is as follows, and further details can be found in Deep Model Reference Adaptive Control
Flight Results
We used an off the shelf available Parrot Mambo Quadrotor to experiment with DMRAC control architecture in the VICON facility at the University of Illinois CSL Illinois Robotics Lab.
Cross Wind Disturbance
In this experiment the controller is tasked to maintain a circular trajectory tracking under a cross wind. We attached a cloth underneath the quadrotor, under the cross wind flapping of this cloth introduced nonlinear disturbance torque on the vehicle apart from side ward force from cross wind. The controller task is to track the trajectory under cross winds.
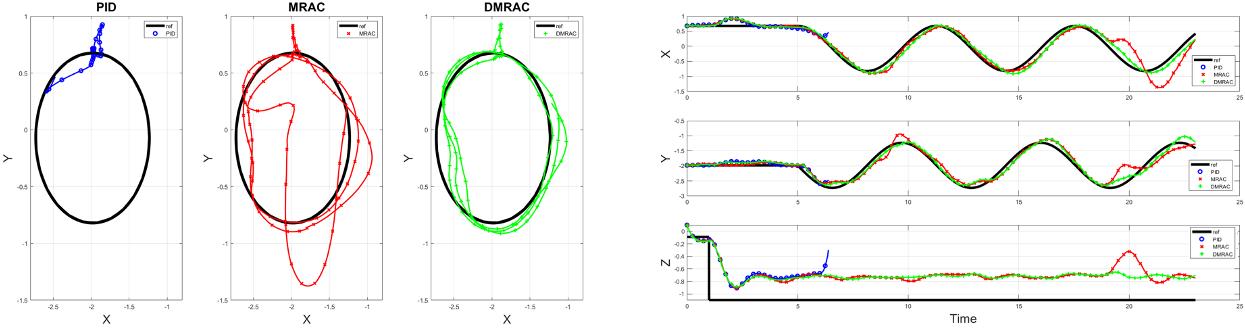
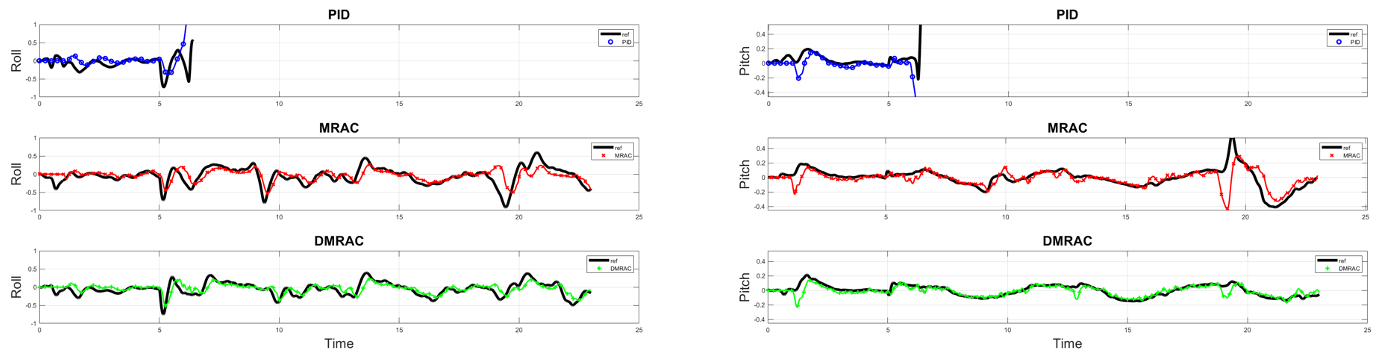
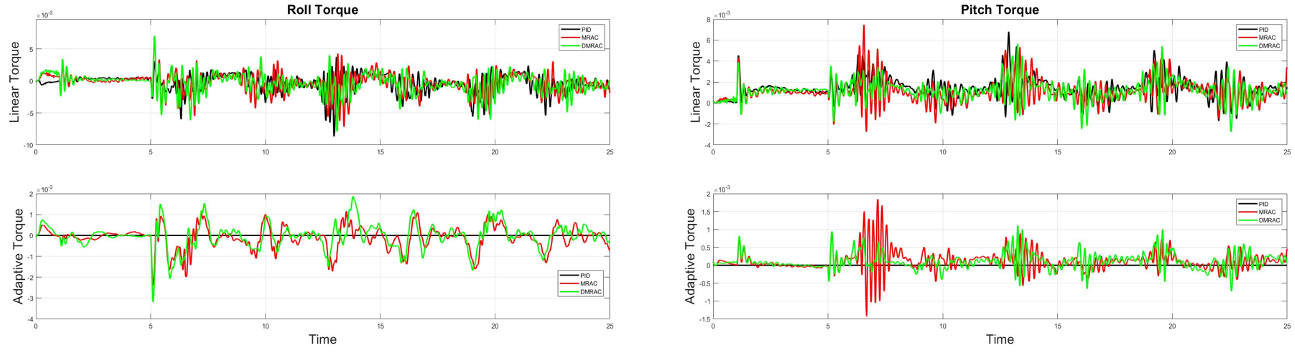
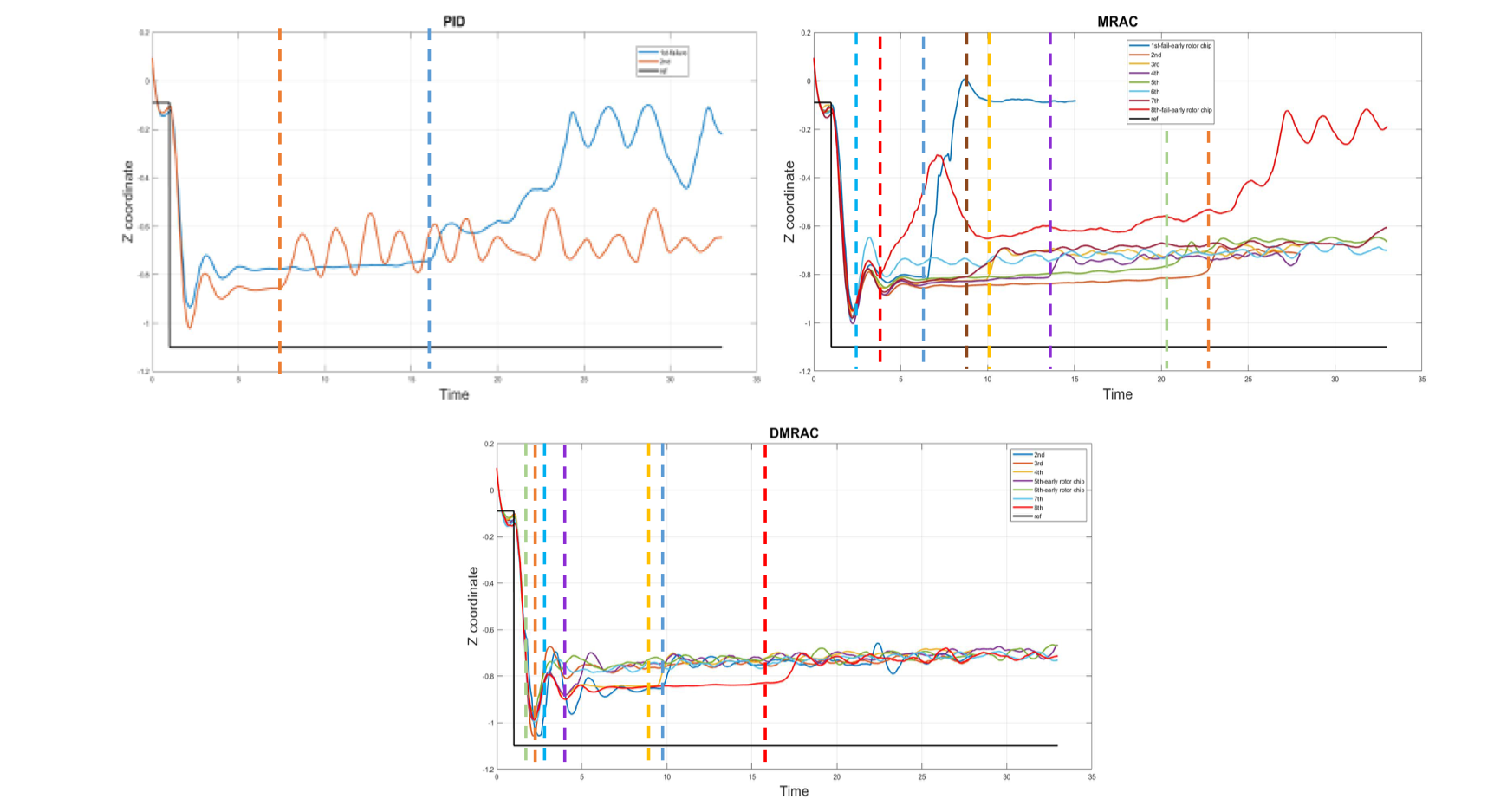
Fault Tolerant Control
In this experiment the controller handles a rotor blade breaking in middle of the flight (Listen to rotor breaking!!). The quadrotor is commanded to maintian a altitude of 1 meter above ground level. The rotor blade breaks in middle of flight and controller task is to maintain the altitude despite the fault.